로봇공학을 위한 공간의 변환 행렬(Transformation Matrix)
로봇공학에서 물체의 위치와 자세를 표현하고 조작하는 것은 가장 기본적이면서도 중요한 작업입니다. 본 문서는 2차원 평면과 3차원 공간에서의 변환 행렬을 체계적으로 설명하며, 회전(Rotation), 병진(Translation), 그리고 이들의 조합을 수학적으로 엄밀하게 다룹니다.
Part II: 3D 변환
Part II: 3D 변환
8. 3D 좌표계와 회전
8.1 3D 좌표계의 정의
3차원 공간에서 한 점의 위치는 세 개의 좌표 $(x, y, z)$로 표현됩니다. 로봇공학에서는 주로 오른손 좌표계(Right-Hand Coordinate System)를 사용합니다[1].
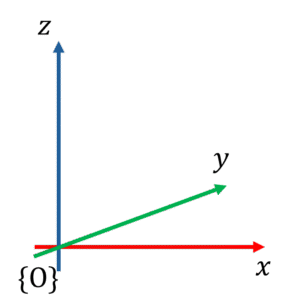
오른손 법칙(Right-Hand Rule):
- 오른손의 엄지(X축), 검지(Y축), 중지(Z축) 방향
- 외적 방향 결정: $\mathbf{x} \times \mathbf{y} = \mathbf{z}$
8.2 3D 벡터의 표현
3D 공간의 점 또는 벡터는 다음과 같이 표현됩니다:
$$ \mathbf{p} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} $$
8.3 3D 회전의 복잡성
2D 회전은 단일 각도 $\theta$로 완전히 정의되지만, 3D 회전은 3개의 독립적인 파라미터가 필요합니다. 이는 3D 회전이 SO(3) 군을 형성하며, 3차원 다양체(3-dimensional manifold)를 이루기 때문입니다[2].
3D 회전을 표현하는 여러 방법:
- 회전 행렬(Rotation Matrix): 9개 원소, 6개 제약 조건 → 3 DOF
- 오일러 각(Euler Angles): 3개의 각도
- 축-각(Axis-Angle): 회전축 벡터(3) + 회전 각도(1) → 4개 파라미터, 1개 제약
- 쿼터니언(Quaternion): 4개 파라미터, 1개 제약 조건
8.4 3D 회전축
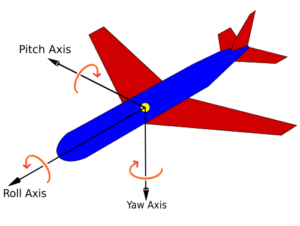
3D 공간에서는 세 개의 주축(Principal Axes) 중심으로 회전할 수 있습니다:
- X축 중심 회전: Roll (롤)
- Y축 중심 회전: Pitch (피치)
- Z축 중심 회전: Yaw (요)
-
9. 3D 회전 행렬
9.1 기본 회전 행렬
3D 공간에서 각 주축을 중심으로 한 회전 행렬을 유도합니다.
(1) X축 중심 회전 (Roll)
X축을 중심으로 각도 $\alpha$만큼 회전:
$$ \mathbf{R}_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha \\ 0 & \sin\alpha & \cos\alpha \end{bmatrix} $$
유도: X축은 고정되고, YZ 평면에서 2D 회전이 발생
(2) Y축 중심 회전 (Pitch)
Y축을 중심으로 각도 $\beta$만큼 회전:
$$ \mathbf{R}_y(\beta) = \begin{bmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \end{bmatrix} $$
⚠️ 주의: $\sin\beta$의 위치가 다릅니다! (오른손 좌표계에서 양의 회전 방향 유지)
(3) Z축 중심 회전 (Yaw)
Z축을 중심으로 각도 $\gamma$만큼 회전:
$$ \mathbf{R}_z(\gamma) = \begin{bmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} $$
유도: Z축은 고정되고, XY 평면에서 2D 회전이 발생 (2D 회전 행렬과 동일)
9.2 3D 회전 행렬의 성질
3D 회전 행렬 $\mathbf{R} \in SO(3)$는 다음을 만족합니다:
(1) 직교 정규성(Orthonormality)
$$ \mathbf{R}^T \mathbf{R} = \mathbf{R} \mathbf{R}^T = \mathbf{I}_{3×3} $$
각 열과 행은 단위 정규 직교 벡터(Orthonormal Vectors)입니다:
$$ \mathbf{R} = \begin{bmatrix} | & | & | \\ \mathbf{r}_1 & \mathbf{r}_2 & \mathbf{r}_3 \\ | & | & | \end{bmatrix} $$
- $|\mathbf{r}_i| = 1$ (단위 벡터)
- $\mathbf{r}_i \cdot \mathbf{r}_j = 0, \quad i \neq j$ (직교)
- $\mathbf{r}_1 \times \mathbf{r}_2 = \mathbf{r}_3$ (오른손 법칙)
(2) 행렬식
$$ \det(\mathbf{R}) = +1 $$
이는 회전이 방향 보존 변환(Orientation-Preserving)임을 의미합니다.
$\det(\mathbf{R}) = -1$인 경우는 반사(Reflection)를 포함하며, SO(3)에 속하지 않습니다.
(3) 역행렬
$$ \mathbf{R}^{-1} = \mathbf{R}^T $$
따라서 역회전은 단순히 전치 행렬을 취하면 됩니다:
$$ \mathbf{R}_x(\alpha)^{-1} = \mathbf{R}_x(\alpha)^T = \mathbf{R}_x(-\alpha) $$
(4) 길이와 각도 보존
- 거리 보존: $|\mathbf{R}\mathbf{p}_1 – \mathbf{R}\mathbf{p}_2| = |\mathbf{p}_1 – \mathbf{p}_2|$
- 각도 보존: 두 벡터 사이의 각도가 회전 후에도 유지
- 외적 보존: $\mathbf{R}(\mathbf{a} \times \mathbf{b}) = (\mathbf{R}\mathbf{a}) \times (\mathbf{R}\mathbf{b})$
(5) 군 구조
SO(3) = {$\mathbf{R} \in \mathbb{R}^{3 \times 3} : \mathbf{R}^T\mathbf{R} = \mathbf{I}, \det(\mathbf{R}) = 1$}
- 닫힘: $\mathbf{R}_1, \mathbf{R}_2 \in SO(3) \Rightarrow \mathbf{R}_1\mathbf{R}_2 \in SO(3)$
- 결합법칙: 행렬 곱셈은 결합법칙 만족
- 항등원: $\mathbf{I} \in SO(3)$
- 역원: $\mathbf{R} \in SO(3) \Rightarrow \mathbf{R}^T \in SO(3)$
9.3 회전 행렬의 기하학적 의미
회전 행렬의 각 열은 회전된 좌표계의 기저 벡터를 나타냅니다:
$$ {}^A\mathbf{R}_B = \begin{bmatrix} | & | & | \\ {}^A\mathbf{x}_B & {}^A\mathbf{y}_B & {}^A\mathbf{z}_B \\ | & | & | \end{bmatrix} $$
- 첫 번째 열 ${}^A\mathbf{x}_B$: 좌표계 {A}에서 본 좌표계 {B}의 X축 방향
- 두 번째 열 ${}^A\mathbf{y}_B$: 좌표계 {A}에서 본 좌표계 {B}의 Y축 방향
- 세 번째 열 ${}^A\mathbf{z}_B$: 좌표계 {A}에서 본 좌표계 {B}의 Z축 방향
9.4 특수한 회전 행렬
자주 사용되는 회전:
90° X축 회전: $$ \mathbf{R}_x(90°) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix} $$
90° Y축 회전: $$ \mathbf{R}_y(90°) = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{bmatrix} $$
90° Z축 회전:
$$ \mathbf{R}_z(90°) = \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$
180° 회전 (각 축): $$ \mathbf{R}_x(180°) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{bmatrix}, \quad \mathbf{R}_y(180°) = \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{bmatrix}, \quad \mathbf{R}_z(180°) = \begin{bmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$
10. 오일러 각
10.1 오일러 각의 정의
오일러 각(Euler Angles)은 3D 회전을 세 번의 연속적인 회전으로 표현하는 방법입니다[3]. 직관적이고 이해하기 쉬워 로봇공학, 항공우주, 컴퓨터 그래픽스 등에서 널리 사용됩니다.
10.2 오일러 각의 종류
총 12가지의 오일러 각 표현이 가능하며, 크게 두 가지로 분류됩니다:
-
Proper Euler Angles (고유 오일러 각): 동일한 축을 두 번 사용
- ZXZ, XYX, YZY, ZYZ, XZX, YXY (6가지)
-
Tait-Bryan Angles (테이트-브라이언 각): 세 개의 서로 다른 축 사용
- XYZ, YZX, ZXY, XZY, ZYX, YXZ (6가지)
로봇공학에서 가장 많이 사용되는 표현:
- ZYX Euler Angles (Roll-Pitch-Yaw)
- ZYZ Euler Angles
10.3 ZYX 오일러 각 (Roll-Pitch-Yaw)
항공우주 및 로봇공학에서 가장 널리 사용되는 표현입니다[4].
회전 순서:
- Z축 중심 $\psi$ (Yaw, 요) 회전
- Y축 중심 $\theta$ (Pitch, 피치) 회전
- X축 중심 $\phi$ (Roll, 롤) 회전
합성 회전 행렬:
$$ \mathbf{R}_{ZYX}(\phi, \theta, \psi) = \mathbf{R}_x(\phi) \mathbf{R}_y(\theta) \mathbf{R}_z(\psi) $$
전개하면:
$$ \mathbf{R}_{ZYX} = \begin{bmatrix} c_\theta c_\psi & -c_\theta s_\psi & s_\theta \\\\ s_\phi s_\theta c_\psi + c_\phi s_\psi & -s_\phi s_\theta s_\psi + c_\phi c_\psi & -s_\phi c_\theta \\\\ -c_\phi s_\theta c_\psi + s_\phi s_\psi & c_\phi s_\theta s_\psi + s_\phi c_\psi & c_\phi c_\theta \end{bmatrix} $$
여기서:
– $c_\alpha = \cos\alpha$, $s_\alpha = \sin\alpha$ (간략 표기)
– $\phi$: Roll, $\theta$: Pitch, $\psi$: Yaw
10.4 ZYZ 오일러 각
고유 오일러 각의 대표적인 예로, 많은 로봇 제어기에서 사용됩니다.
회전 순서:
- Z축 중심 $\alpha$ 회전
- Y축 중심 $\beta$ 회전
- Z축 중심 $\gamma$ 회전
합성 회전 행렬: $$ \mathbf{R}_{ZYZ}(\alpha, \beta, \gamma) = \mathbf{R}_z(\alpha) \mathbf{R}_y(\beta) \mathbf{R}_z(\gamma) $$
전개하면:
$$ \mathbf{R}_{ZYZ} = \begin{bmatrix} c_\alpha c_\beta c_\gamma – s_\alpha s_\gamma & -c_\alpha c_\beta s_\gamma – s_\alpha c_\gamma & c_\alpha s_\beta \\ s_\alpha c_\beta c_\gamma + c_\alpha s_\gamma & -s_\alpha c_\beta s_\gamma + c_\alpha c_\gamma & s_\alpha s_\beta \\ -s_\beta c_\gamma & s_\beta s_\gamma & c_\beta \end{bmatrix} $$
10.5 회전 행렬에서 오일러 각 추출
주어진 회전 행렬 $\mathbf{R}$에서 오일러 각을 추출하는 것을 역 기구학(Inverse Kinematics) 문제라고 합니다.
ZYX (Roll-Pitch-Yaw) 추출
회전 행렬:
$$ \mathbf{R} = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} $$
추출 공식:
$$ \begin{align} heta &= \arctan2(r_{13}, \sqrt{r_{11}^2 + r_{12}^2}) \quad &\text{(Pitch)} \\\\ \psi &= \arctan2(-r_{12}, r_{11}) \quad &\text{(Yaw)} \\\\ \phi &= \arctan2(-r_{23}, r_{33}) \quad &\text{(Roll)} \end{align} $$
ZYZ 추출
$$ \begin{align} \beta &= \arctan2(\sqrt{r_{31}^2 + r_{32}^2}, r_{33}) \\\\ \alpha &= \arctan2(r_{23}, r_{13}) \\\\ \gamma &= \arctan2(r_{32}, -r_{31}) \end{align} $$
10.6 짐벌 락(Gimbal Lock)
짐벌 락(Gimbal Lock)은 오일러 각의 가장 큰 문제점으로, 특정 자세에서 한 자유도를 잃어버리는 현상입니다[5].
ZYX 오일러 각에서의 짐벌 락:
Pitch 각이 $\pm 90°$일 때 발생:
$$ heta = \pm \frac{\pi}{2} $$
이 경우 $\mathbf{R}_{ZYX}$은:
$$ \mathbf{R}_{ZYX}(\phi, 90°, \psi) = \begin{bmatrix} 0 & 0 & 1 \\\\ s_{\phi+\psi} & c_{\phi+\psi} & 0 \\\\ -c_{\phi+\psi} & s_{\phi+\psi} & 0 \end{bmatrix} $$
Roll($\phi$)과 Yaw($\psi$)가 합 $\phi + \psi$로만 나타나므로, 개별 값을 구분할 수 없습니다.
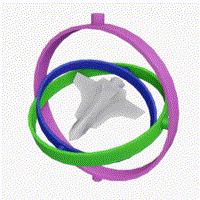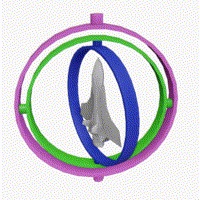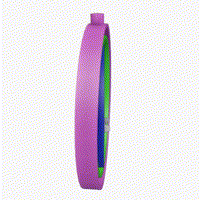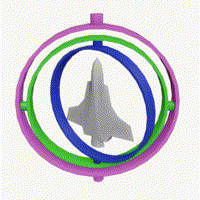
짐벌 락의 영향:
- 특이점(Singularity) 발생
- 수치 불안정성
- 보간(Interpolation) 시 비정상적인 경로
- 제어 불능 상태 가능
해결 방법:
- 쿼터니언 사용 (다음 섹션에서 다룸)
- 다른 오일러 각 표현 선택
- 특이점 회피 알고리즘
10.7 오일러 각의 장단점
장점:
- ✅ 직관적이고 이해하기 쉬움
- ✅ 3개의 파라미터로 간결한 표현
- ✅ 사람이 읽고 해석하기 용이
- ✅ 메모리 효율적
단점:
- ❌ 짐벌 락 문제
- ❌ 12가지 표현법으로 혼란 가능
- ❌ 보간이 어려움
- ❌ 특이점에서 수치 불안정
- ❌ 합성이 비직관적 (행렬 곱셈 필요)
11. 3D 강체 변환
11.1 3D 동차 좌표계
3D 점 $(x, y, z)$를 4차원 동차 좌표로 확장:
$$ \begin{bmatrix} x \ y \ z \end{bmatrix} \rightarrow \begin{bmatrix} x \ y \ z \ 1 \end{bmatrix} $$
11.2 3D 동차 변환 행렬
동차 변환 행렬(Homogeneous Transformation Matrix) $\mathbf{T} \in SE(3)$:
$$ \mathbf{T} = \begin{bmatrix} \mathbf{R} & \mathbf{p} \\ \mathbf{0}^T & 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & p_x \\ r_{21} & r_{22} & r_{23} & p_y \\ r_{31} & r_{32} & r_{33} & p_z \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
여기서:
- $\mathbf{R} \in SO(3)$: $3 \times 3$ 회전 행렬 (9개 원소, 6개 제약 → 3 DOF)
- $\mathbf{p} \in \mathbb{R}^3$: $3 \times 1$ 병진 벡터 (3 DOF)
- $\mathbf{0}^T = \begin{bmatrix} 0 & 0 & 0 \end{bmatrix}$: $1 \times 3$ 영벡터
- $1$: 스칼라
전체 자유도: 3 (회전) + 3 (병진) = 6 DOF
11.3 좌표 변환
좌표계 {B}에서 표현된 점을 좌표계 {A}에서 표현:
$$ \begin{bmatrix} {}^A\mathbf{p} \\ 1 \end{bmatrix} = {}^A\mathbf{T}_B \begin{bmatrix} {}^B\mathbf{p} \\ 1 \end{bmatrix} $$
전개하면:
$$ {}^A\mathbf{p} = {}^A\mathbf{R}_B \cdot {}^B\mathbf{p} + {}^A\mathbf{p}_{B,org} $$
11.4 3D 역변환
$$ \mathbf{T}^{-1} = \begin{bmatrix} \mathbf{R} & \mathbf{p} \\ \mathbf{0}^T & 1 \end{bmatrix}^{-1} = \begin{bmatrix} \mathbf{R}^T & -\mathbf{R}^T\mathbf{p} \\ \mathbf{0}^T & 1 \end{bmatrix} $$
계산 효율:
- 일반 $4 \times 4$ 역행렬: $O(n^3) \approx 64$ 연산
- SE(3) 역변환: 전치 + 행렬-벡터 곱 ≈ 9 + 9 = 18 연산
11.5 변환의 합성
세 좌표계 {A}, {B}, {C}:
$$ {}^A\mathbf{T}_C = {}^A\mathbf{T}_B \cdot {}^B\mathbf{T}_C $$
⚠️ 주의: 오른쪽에서 왼쪽 순서로 적용!
11.6 SE(3) 군의 성질
SE(3) = {$\mathbf{T} = \begin{bmatrix} \mathbf{R} & \mathbf{p} \\ \mathbf{0}^T & 1 \end{bmatrix} : \mathbf{R} \in SO(3), \mathbf{p} \in \mathbb{R}^3$}
- 닫힘: $\mathbf{T}_1, \mathbf{T}_2 \in SE(3) \Rightarrow \mathbf{T}_1 \mathbf{T}_2 \in SE(3)$
- 결합법칙: 행렬 곱셈
- 항등원: $\mathbf{I}_{4 \times 4}$
- 역원: 위에서 정의한 역변환
11.7 로봇 기구학에서의 응용
전방 기구학(Forward Kinematics):
n-링크 로봇 팔의 엔드 이펙터 위치:
$$ {}^0\mathbf{T}_n = {}^0\mathbf{T}_1 \cdot {}^1\mathbf{T}_2 \cdot {}^2\mathbf{T}_3 \cdots {}^{n-1}\mathbf{T}_n $$
각 ${}^{i-1}\mathbf{T}_i$는 조인트 $i$의 변환 행렬입니다.

12. 3D 실전 예제
12.1 예제 1: 3D 기본 회전
문제: 점 $P(1, 0, 0)$을 Z축 중심으로 90° 회전한 후의 위치는?
풀이:
$$ \mathbf{R}_z(90°) = \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$
$$ \mathbf{p}’ = \mathbf{R}_z(90°) \mathbf{p} = \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} $$
답: $(0, 1, 0)$
12.2 예제 2: 복합 회전
문제: 점 $(1, 1, 1)$을 먼저 Z축 중심 45° 회전, 그 다음 X축 중심 30° 회전시킬 때 최종 위치는?
풀이:
$$ \mathbf{R} = \mathbf{R}_x(30°) \cdot \mathbf{R}_z(45°) $$
$$ \mathbf{R}_z(45°) = \begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} & 0 \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad \mathbf{R}_x(30°) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{\sqrt{3}}{2} & -\frac{1}{2} \\ 0 & \frac{1}{2} & \frac{\sqrt{3}}{2} \end{bmatrix} $$
먼저 Z축 회전:
$$ \mathbf{p}_1 = \mathbf{R}_z(45°) \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ \sqrt{2} \\ 1 \end{bmatrix} $$
다음 X축 회전:
$$ \mathbf{p}’ = \mathbf{R}_x(30°) \mathbf{p}_1 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{\sqrt{3}}{2} & -\frac{1}{2} \\ 0 & \frac{1}{2} & \frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} 0 \\ \sqrt{2} \\ 1 \end{bmatrix} $$
$$ = \begin{bmatrix} 0 \\ \frac{\sqrt{3}}{2} \cdot \sqrt{2} – \frac{1}{2} \\ \frac{1}{2} \cdot \sqrt{2} + \frac{\sqrt{3}}{2} \end{bmatrix} \approx \begin{bmatrix} 0 \\ 0.726 \\ 1.573 \end{bmatrix} $$
답: 약 $(0, 0.726, 1.573)$
12.3 예제 3: 오일러 각에서 회전 행렬
문제: ZYX 오일러 각이 Roll=30°, Pitch=45°, Yaw=60°일 때 회전 행렬은?
풀이:
$$ \mathbf{R} = \mathbf{R}_x(30°) \mathbf{R}_y(45°) \mathbf{R}_z(60°) $$
각 행렬:
$$ \mathbf{R}_z(60°) = \begin{bmatrix} 0.5 & -0.866 & 0 \\ 0.866 & 0.5 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$
$$ \mathbf{R}_y(45°) = \begin{bmatrix} 0.707 & 0 & 0.707 \\ 0 & 1 & 0 \\ -0.707 & 0 & 0.707 \end{bmatrix} $$
$$ \mathbf{R}_x(30°) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0.866 & -0.5 \\ 0 & 0.5 & 0.866 \end{bmatrix} $$
곱셈 수행 (중간 과정 생략):
$$ \mathbf{R} \approx \begin{bmatrix} 0.354 & -0.612 & 0.707 \\ 0.927 & 0.307 & -0.217 \\ -0.127 & 0.729 & 0.673 \end{bmatrix} $$
검증: $\mathbf{R}^T\mathbf{R} = \mathbf{I}$, $\det(\mathbf{R}) = 1$ ✓
12.4 예제 4: 회전 행렬에서 오일러 각 추출
문제: 다음 회전 행렬에서 ZYX 오일러 각을 추출하라:
$$ \mathbf{R} = \begin{bmatrix} 0.707 & -0.612 & 0.354 \\ 0.707 & 0.612 & -0.354 \\ 0 & 0.500 & 0.866 \end{bmatrix} $$
풀이:
ZYX 추출 공식 적용:
$$ heta = \arctan2(r_{13}, \sqrt{r_{11}^2 + r_{12}^2}) = \arctan2(0.354, \sqrt{0.707^2 + 0.612^2}) $$
$$ = \arctan2(0.354, 0.936) \approx 20.7° $$
$$ \psi = \arctan2(-r_{12}, r_{11}) = \arctan2(-(-0.612), 0.707) = \arctan2(0.612, 0.707) \approx 40.9° $$
$$ \phi = \arctan2(-r_{23}, r_{33}) = \arctan2(-(-0.354), 0.866) = \arctan2(0.354, 0.866) \approx 22.2° $$
답: Roll ≈ 22.2°, Pitch ≈ 20.7°, Yaw ≈ 40.9°
12.5 예제 5: 3D 로봇 팔 기구학
문제: 3링크 공간 로봇 팔이 있다. 각 링크는 Z축 조인트(회전)를 가지며:
- 링크 1: 길이 2 (Z방향), 회전 $\theta_1 = 30°$
- 링크 2: 길이 1.5 (Z방향), 회전 $\theta_2 = 45°$
- 링크 3: 길이 1 (Z방향), 회전 $\theta_3 = 60°$
엔드 이펙터의 최종 위치는?
풀이:
각 링크의 변환 행렬 (DH 파라미터 간략화):
$$ {}^{i-1}\mathbf{T}_i = \begin{bmatrix} \cos\theta_i & -\sin\theta_i & 0 & 0 \\ \sin\theta_i & \cos\theta_i & 0 & 0 \\ 0 & 0 & 1 & L_i \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
$$ {}^0\mathbf{T}_1 = \begin{bmatrix} 0.866 & -0.5 & 0 & 0 \\ 0.5 & 0.866 & 0 & 0 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
$$ {}^1\mathbf{T}_2 = \begin{bmatrix} 0.707 & -0.707 & 0 & 0 \\ 0.707 & 0.707 & 0 & 0 \\ 0 & 0 & 1 & 1.5 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
$$ {}^2\mathbf{T}_3 = \begin{bmatrix} 0.5 & -0.866 & 0 & 0 \\ 0.866 & 0.5 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
$$ {}^0\mathbf{T}_3 = {}^0\mathbf{T}_1 \cdot {}^1\mathbf{T}_2 \cdot {}^2\mathbf{T}_3 $$
최종 위치 (병진 성분):
$$ \mathbf{p} = \begin{bmatrix} 0 \\ 0 \\ 4.5 \end{bmatrix} $$
(모든 회전이 Z축이므로 XY 평면 위치는 원점, Z 방향으로만 누적)
답: 엔드 이펙터 위치는 $(0, 0, 4.5)$
3D 변환 정리 및 핵심 공식
3D 회전 행렬
X축 회전: $$ \mathbf{R}_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha \\ 0 & \sin\alpha & \cos\alpha \end{bmatrix} $$
Y축 회전: $$ \mathbf{R}_y(\beta) = \begin{bmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \end{bmatrix} $$
Z축 회전: $$ \mathbf{R}_z(\gamma) = \begin{bmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} $$
ZYX 오일러 각
회전 행렬: $$ \mathbf{R}_{ZYX}(\phi, \theta, \psi) = \mathbf{R}_x(\phi) \mathbf{R}_y(\theta) \mathbf{R}_z(\psi) $$
역변환:
$$ \begin{align} \theta &= \arctan2(r_{13}, \sqrt{r_{11}^2 + r_{12}^2}) \\ \psi &= \arctan2(-r_{12}, r_{11}) \\ \phi &= \arctan2(-r_{23}, r_{33}) \end{align} $$
3D 동차 변환
SE(3) 행렬:
$$ \mathbf{T} = \begin{bmatrix} \mathbf{R}_{3\times3} & \mathbf{p}_{3\times1} \\ \mathbf{0}_{1\times3}^T & 1 \end{bmatrix} $$
역변환:
$$ \mathbf{T}^{-1} = \begin{bmatrix} \mathbf{R}^T & -\mathbf{R}^T\mathbf{p} \\ \mathbf{0}^T & 1 \end{bmatrix} $$
자유도 요약
| 공간 | 회전 DOF | 병진 DOF | 전체 DOF |
|---|---|---|---|
| 2D | 1 (각도) | 2 (x, y) | 3 |
| 3D | 3 (roll, pitch, yaw) | 3 (x, y, z) | 6 |
참고문헌
[1] Murray, Richard M., et al. A Mathematical Introduction to Robotic Manipulation. CRC Press, 1994.
[2] Craig, John J. Introduction to Robotics: Mechanics and Control. 4th ed. Pearson, 2017.
[3] Spong, Mark W., Seth Hutchinson, and Mathukumalli Vidyasagar. Robot Modeling and Control. 2nd ed. Wiley, 2020.
[4] Lynch, Kevin M., and Frank C. Park. Modern Robotics: Mechanics, Planning, and Control. Cambridge University Press, 2017.
[5] Siciliano, Bruno, et al. Robotics: Modelling, Planning and Control. Springer, 2009.
[6] Paul, Richard P. Robot Manipulators: Mathematics, Programming, and Control. MIT Press, 1981.
[7] Goldstein, Herbert, Charles Poole, and John Safko. Classical Mechanics. 3rd ed. Addison-Wesley, 2002.
[8] Strang, Gilbert. Introduction to Linear Algebra. 5th ed. Wellesley-Cambridge Press, 2016.
[9] Dai, Jian S. “Euler-Rodrigues formula variations, quaternion conjugation and intrinsic connections.” Mechanism and Machine Theory 92 (2015): 144-152.
[10] Rodrigues, Olinde. “Des lois géométriques qui régissent les déplacements d’un système solide dans l’espace.” Journal de Mathématiques Pures et Appliquées 5 (1840): 380-440.
[11] Ball, Robert Stawell. A Treatise on the Theory of Screws. Cambridge University Press, 1900.
[12] Selig, J. M. Geometric Fundamentals of Robotics. 2nd ed. Springer, 2005.
추가 학습 자료
온라인 강의
- MIT OpenCourseWare: “Introduction to Robotics” (Prof. John Leonard)
- Coursera: “Modern Robotics” (Northwestern University)
- edX: “Robot Mechanics and Control” (Seoul National University)
소프트웨어 도구
- MATLAB Robotics Toolbox (Peter Corke)
- Python Robotics (Atsushi Sakai) – https://github.com/AtsushiSakai/PythonRobotics
- ROS (Robot Operating System) – TF (Transform) 라이브러리
추천 도서
- Corke, Peter. Robotics, Vision and Control. 2nd ed. Springer, 2017.
- Tsai, Lung-Wen. Robot Analysis: The Mechanics of Serial and Parallel Manipulators. Wiley, 1999.
본 문서는 로봇공학의 핵심인 변환 행렬, 고급 회전 표현, 스크류 이론에 대한 종합적인 학습을 위해 작성되었습니다. 2D/3D 기초부터 쿼터니언, 리 군/리 대수, 제품 지수 공식까지 체계적으로 다루며, 현대 로봇공학의 수학적 기반을 제공합니다.
작성일: 2024년 12월
최종 수정일: 2024년 12월 14일
키워드: 로봇공학, 변환 행렬, 회전 행렬, 쿼터니언, 스크류 이론, 리 군, 리 대수, 트위스트, 렌치, 제품 지수 공식, 동차 좌표계, 강체 변환, SE(2), SE(3), SO(3), 기구학, 자코비안
