평면에서의 회전변환

우리는 일반적으로 평면에서 무엇인가를 정의하기 위해서 기준 좌표계를 잡는다.

 

기준 좌표계를 기준으로 어떤 물체를 표현할 때는 회전((Rotation))과 병진((Translation)) 표현할 수 있다. 

 

Fig 1. 평면에서의 물체 정의

 

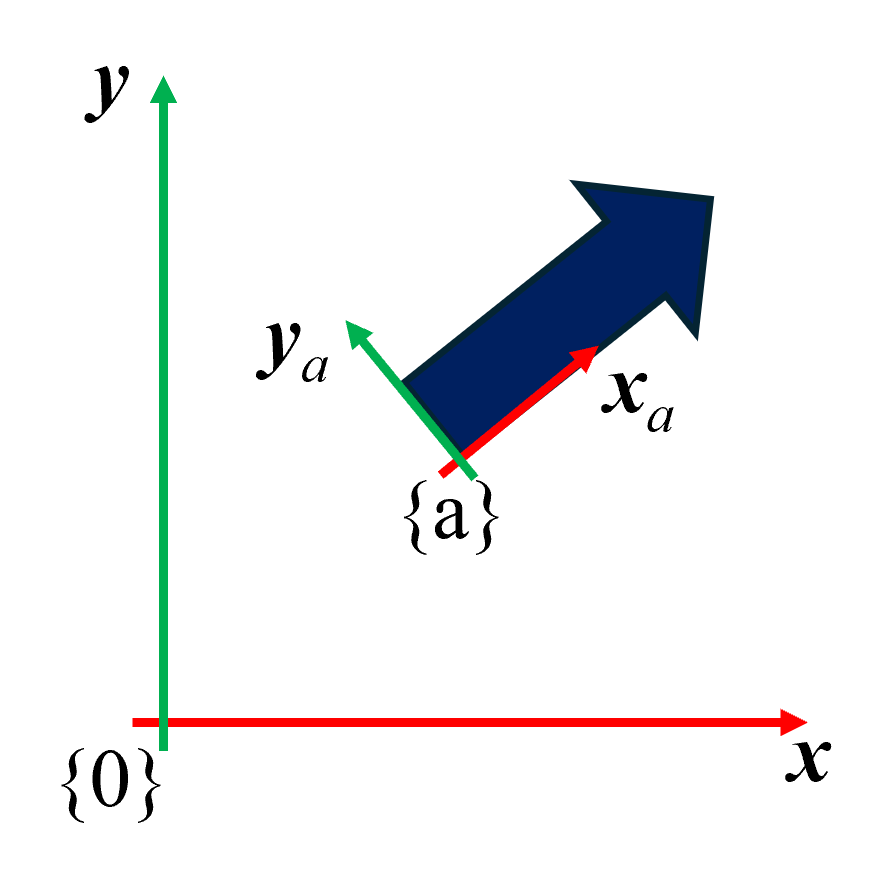
Fig 1.과 같이 화살표를 정의하기 위해서는 기준 좌표계{0}를 기준으로 {a}좌표계를 정의할 수 있다. 

 

여기서는 {a}좌표계를 정의하기 위해서 회전을 어떻게 표현하는지 설명하고자 한다.

 

Fig 2. 평면에서의 회전 변환

 

Fig 2.는 평면에서 회전 변환를 표현하기 위한 그림이다. $p_2$점은 $p_1$점에서 $\alpha$만큼 더 회전 한 점이다.

 

따라서 $p_1$점과 $p_2$점은 각각 다음과 같이 표현할 수 있다.

 

$p_1 = \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} = \begin{bmatrix} l*cos(\theta) \\ l*sin(\theta) \end{bmatrix}$

$p_2 = \begin{bmatrix} x_2 \\ y_2 \end{bmatrix} = \begin{bmatrix} l*cos(\theta + \alpha) \\ l*sin(\theta + \alpha) \end{bmatrix} $

 

가 된다. 이 때, $p_2$를 풀어서 쓰면 다음과 같이 표현할 수 있다.

 

$\begin{bmatrix} x_2 \\ y_2 \end{bmatrix} = l*\begin{bmatrix} cos(\theta)*cos(\alpha) - sin(\theta)*sin(\alpha) \\ sin(\theta)*cos(\alpha)+cos(\theta)*sin(\alpha) \end{bmatrix}$

 

여기서, $l*cos(\theta) = x_1$이고, $l*sin(\theta) = y_1$이 되므로, 다음과 같이 표현할 수 있다.

 

$ \begin{bmatrix}
x_2 \\ y_2 \end{bmatrix} = \begin{bmatrix}
cos(\alpha)*x_1 - sin(\alpha)*y_1 \\ cos(\alpha)*y1+sin(\alpha)*x_1 \end{bmatrix} = \begin{bmatrix}
cos(\alpha) && - sin(\alpha) \\ sin(\alpha) && cos(\alpha) \end{bmatrix} \begin{bmatrix}
x_1 \\ y_21 \end{bmatrix}$

 

즉, [$x_2$ $y_2$]$^T$와 [$x_1$ $y_1$]$^T$의 관계식이 성립 된다.

 

여기서 $\begin{bmatrix}
cos(\alpha) && - sin(\alpha) \\ sin(\alpha) && cos(\alpha) \end{bmatrix} $가 회전 변환 행렬이 된다. 

 

이 때, 이 식을 3차원으로 확장하면 z축을 중심으로 회전하는 식이 되고 다음과 같이 표현할 수 있다.

 

$\begin{bmatrix}
cos(\alpha) && - sin(\alpha) && 0 \\ sin(\alpha) && cos(\alpha) && 0 \\ 0 && 0 && 1 \end{bmatrix} $

 

같은 방법으로 x축과 y축을 중심으로 회전은 다음과 같이 표현할 수 있다.

 

1) x축을 중심으로 회전

$\begin{bmatrix}
1 && 0 && 0 \\ 0 && cos(\alpha) && -sin(\alpha) \\ 0 && sin(\alpha) && cos(\alpha) \end{bmatrix} $

 

2) y축을 중심으로 회전

$\begin{bmatrix} cos(\alpha) && 0 && sin(\alpha) \\ 0 && 1 && 0 \\ -sin(\alpha) && 0 && cos(\alpha) \end{bmatrix} $

 

이 때, sin($\alpha$)의 부호가 y축을 중심으로 회전일 때 반대로 붙는 다는 점을 유의해야 한다.